The Law of Accelerating Returns
by Brett Rampat, kurzweilai.netMarch 7th 2001
We can organize these observations into what I call the law of accelerating returns as follows:
- Evolution applies positive feedback in that the more capable methods resulting from one stage of evolutionary progress are used to create the next stage. As a result, the
- rate of progress of an evolutionary process increases exponentially over time. Over time, the “order” of the information embedded in the evolutionary process (i.e., the measure of how well the information fits a purpose, which in evolution is survival) increases.
- A correlate of the above observation is that the “returns” of an evolutionary process (e.g., the speed, cost-effectiveness, or overall “power” of a process) increase exponentially over time.
- In another positive feedback loop, as a particular evolutionary process (e.g., computation) becomes more effective (e.g., cost effective), greater resources are deployed toward the further progress of that process. This results in a second level of exponential growth (i.e., the rate of exponential growth itself grows exponentially).
- Biological evolution is one such evolutionary process.
- Technological evolution is another such evolutionary process. Indeed, the emergence of the first technology creating species resulted in the new evolutionary process of technology. Therefore, technological evolution is an outgrowth of–and a continuation of–biological evolution.
- A specific paradigm (a method or approach to solving a problem, e.g., shrinking transistors on an integrated circuit as an approach to making more powerful computers) provides exponential growth until the method exhausts its potential. When this happens, a paradigm shift (i.e., a fundamental change in the approach) occurs, which enables exponential growth to continue.
If we apply these principles at the highest level of evolution on Earth, the first step, the creation of cells, introduced the paradigm of biology. The subsequent emergence of DNA provided a digital method to record the results of evolutionary experiments. Then, the evolution of a species who combined rational thought with an opposable appendage (i.e., the thumb) caused a fundamental paradigm shift from biology to technology. The upcoming primary paradigm shift will be from biological thinking to a hybrid combining biological and nonbiological thinking. This hybrid will include “biologically inspired” processes resulting from the reverse engineering of biological brains.
If we examine the timing of these steps, we see that the process has continuously accelerated. The evolution of life forms required billions of years for the first steps (e.g., primitive cells); later on progress accelerated. During the Cambrian explosion, major paradigm shifts took only tens of millions of years. Later on, Humanoids developed over a period of millions of years, and Homo sapiens over a period of only hundreds of thousands of years.
With the advent of a technology-creating species, the exponential pace became too fast for evolution through DNA-guided protein synthesis and moved on to human-created technology. Technology goes beyond mere tool making; it is a process of creating ever more powerful technology using the tools from the previous round of innovation. In this way, human technology is distinguished from the tool making of other species. There is a record of each stage of technology, and each new stage of technology builds on the order of the previous stage.
The first technological steps-sharp edges, fire, the wheel–took tens of thousands of years. For people living in this era, there was little noticeable technological change in even a thousand years. By 1000 A.D., progress was much faster and a paradigm shift required only a century or two. In the nineteenth century, we saw more technological change than in the nine centuries preceding it. Then in the first twenty years of the twentieth century, we saw more advancement than in all of the nineteenth century. Now, paradigm shifts occur in only a few years time. The World Wide Web did not exist in anything like its present form just a few years ago; it didn’t exist at all a decade ago.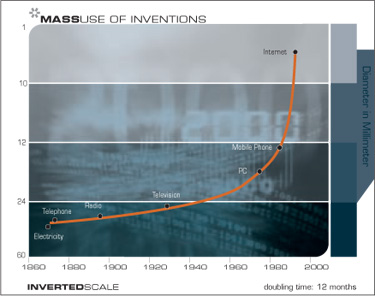
The paradigm shift rate (i.e., the overall rate of technical progress) is currently doubling (approximately) every decade; that is, paradigm shift times are halving every decade (and the rate of acceleration is itself growing exponentially). So, the technological progress in the twenty-first century will be equivalent to what would require (in the linear view) on the order of 200 centuries. In contrast, the twentieth century saw only about 25 years of progress (again at today’s rate of progress) since we have been speeding up to current rates. So the twenty-first century will see almost a thousand times greater technological change than its predecessor.
The Singularity Is Near
To appreciate the nature and significance of the coming “singularity,” it is important to ponder the nature of exponential growth. Toward this end, I am fond of telling the tale of the inventor of chess and his patron, the emperor of China. In response to the emperor’s offer of a reward for his new beloved game, the inventor asked for a single grain of rice on the first square, two on the second square, four on the third, and so on. The Emperor quickly granted this seemingly benign and humble request. One version of the story has the emperor going bankrupt as the 63 doublings ultimately totaled 18 million trillion grains of rice. At ten grains of rice per square inch, this requires rice fields covering twice the surface area of the Earth, oceans included. Another version of the story has the inventor losing his head.
It should be pointed out that as the emperor and the inventor went through the first half of the chess board, things were fairly uneventful. The inventor was given spoonfuls of rice, then bowls of rice, then barrels. By the end of the first half of the chess board, the inventor had accumulated one large field’s worth (4 billion grains), and the emperor did start to take notice. It was as they progressed through the second half of the chessboard that the situation quickly deteriorated. Incidentally, with regard to the doublings of computation, that’s about where we stand now–there have been slightly more than 32 doublings of performance since the first programmable computers were invented during World War II.
This is the nature of exponential growth. Although technology grows in the exponential domain, we humans live in a linear world. So technological trends are not noticed as small levels of technological power are doubled. Then seemingly out of nowhere, a technology explodes into view. For example, when the Internet went from 20,000 to 80,000 nodes over a two year period during the 1980s, this progress remained hidden from the general public. A decade later, when it went from 20 million to 80 million nodes in the same amount of time, the impact was rather conspicuous.
As exponential growth continues to accelerate into the first half of the twenty-first century, it will appear to explode into infinity, at least from the limited and linear perspective of contemporary humans. The progress will ultimately become so fast that it will rupture our ability to follow it. It will literally get out of our control. The illusion that we have our hand “on the plug,” will be dispelled.
Can the pace of technological progress continue to speed up indefinitely? Is there not a point where humans are unable to think fast enough to keep up with it? With regard to unenhanced humans, clearly so. But what would a thousand scientists, each a thousand times more intelligent than human scientists today, and each operating a thousand times faster than contemporary humans (because the information processing in their primarily nonbiological brains is faster) accomplish? One year would be like a millennium. What would they come up with?
Well, for one thing, they would come up with technology to become even more intelligent (because their intelligence is no longer of fixed capacity). They would change their own thought processes to think even faster. When the scientists evolve to be a million times more intelligent and operate a million times faster, then an hour would result in a century of progress (in today’s terms).
This, then, is the Singularity. The Singularity is technological change so rapid and so profound that it represents a rupture in the fabric of human history. Some would say that we cannot comprehend the Singularity, at least with our current level of understanding, and that it is impossible, therefore, to look past its “event horizon” and make sense of what lies beyond.
My view is that despite our profound limitations of thought, constrained as we are today to a mere hundred trillion interneuronal connections in our biological brains, we nonetheless have sufficient powers of abstraction to make meaningful statements about the nature of life after the Singularity. Most importantly, it is my view that the intelligence that will emerge will continue to represent the human civilization, which is already a human-machine civilization. This will be the next step in evolution, the next high level paradigm shift.
To put the concept of Singularity into perspective, let’s explore the history of the word itself. Singularity is a familiar word meaning a unique event with profound implications. In mathematics, the term implies infinity, the explosion of value that occurs when dividing a constant by a number that gets closer and closer to zero. In physics, similarly, a singularity denotes an event or location of infinite power. At the center of a black hole, matter is so dense that its gravity is infinite. As nearby matter and energy are drawn into the black hole, an event horizon separates the region from the rest of the Universe. It constitutes a rupture in the fabric of space and time. The Universe itself is said to have begun with just such a Singularity.
In the 1950s, John Von Neumann was quoted as saying that “the ever accelerating progress of technology…gives the appearance of approaching some essential singularity in the history of the race beyond which human affairs, as we know them, could not continue.” In the 1960s, I. J. Good wrote of an “intelligence explosion,” resulting from intelligent machines designing their next generation without human intervention. In 1986, Vernor Vinge, a mathematician and computer scientist at San Diego State University, wrote about a rapidly approaching technological “singularity” in his science fiction novel, Marooned in Realtime. Then in 1993, Vinge presented a paper to a NASA-organized symposium which described the Singularity as an impending event resulting primarily from the advent of “entities with greater than human intelligence,” which Vinge saw as the harbinger of a run-away phenomenon.
From my perspective, the Singularity has many faces. It represents the nearly vertical phase of exponential growth where the rate of growth is so extreme that technology appears to be growing at infinite speed. Of course, from a mathematical perspective, there is no discontinuity, no rupture, and the growth rates remain finite, albeit extraordinarily large. But from our currently limited perspective, this imminent event appears to be an acute and abrupt break in the continuity of progress. However, I emphasize the word “currently,” because one of the salient implications of the Singularity will be a change in the nature of our ability to understand. In other words, we will become vastly smarter as we merge with our technology.
When I wrote my first book, The Age of Intelligent Machines, in the 1980s, I ended the book with the specter of the emergence of machine intelligence greater than human intelligence, but found it difficult to look beyond this event horizon. Now having thought about its implications for the past 20 years, I feel that we are indeed capable of understanding the many facets of this threshold, one that will transform all spheres of human life.
Consider a few examples of the implications. The bulk of our experiences will shift from real reality to virtual reality. Most of the intelligence of our civilization will ultimately be nonbiological, which by the end of this century will be trillions of trillions of times more powerful than human intelligence. However, to address often expressed concerns, this does not imply the end of biological intelligence, even if thrown from its perch of evolutionary superiority. Moreover, it is important to note that the nonbiological forms will be derivative of biological design. In other words, our civilization will remain human, indeed in many ways more exemplary of what we regard as human than it is today, although our understanding of the term will move beyond its strictly biological origins.
Many observers have nonetheless expressed alarm at the emergence of forms of nonbiological intelligence superior to human intelligence. The potential to augment our own intelligence through intimate connection with other thinking mediums does not necessarily alleviate the concern, as some people have expressed the wish to remain “unenhanced” while at the same time keeping their place at the top of the intellectual food chain. My view is that the likely outcome is that on the one hand, from the perspective of biological humanity, these superhuman intelligences will appear to be their transcendent servants, satisfying their needs and desires. On the other hand, fulfilling the wishes of a revered biological legacy will occupy only a trivial portion of the intellectual power that the Singularity will bring.
Needless to say, the Singularity will transform all aspects of our lives, social, sexual, and economic, which I explore herewith.
Wherefrom Moore’s Law
Before considering further the implications of the Singularity, let’s examine the wide range of technologies that are subject to the law of accelerating returns. The exponential trend that has gained the greatest public recognition has become known as “Moore’s Law.” Gordon Moore, one of the inventors of integrated circuits, and then Chairman of Intel, noted in the mid 1970s that we could squeeze twice as many transistors on an integrated circuit every 24 months. Given that the electrons have less distance to travel, the circuits also run twice as fast, providing an overall quadrupling of computational power.
After sixty years of devoted service, Moore’s Law will die a dignified death no later than the year 2019. By that time, transistor features will be just a few atoms in width, and the strategy of ever finer photolithography will have run its course. So, will that be the end of the exponential growth of computing?
Don’t bet on it.
If we plot the speed (in instructions per second) per $1000 (in constant dollars) of 49 famous calculators and computers spanning the entire twentieth century, we note some interesting observations.
Moore’s Law Was Not the First, but the Fifth Paradigm To Provide Exponential Growth of Computing
Each time one paradigm runs out of steam, another picks up the pace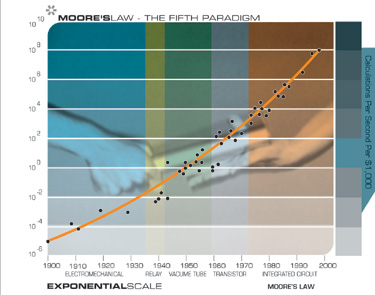
It is important to note that Moore’s Law of Integrated Circuits was not the first, but the fifth paradigm to provide accelerating price-performance. Computing devices have been consistently multiplying in power (per unit of time) from the mechanical calculating devices used in the 1890 U.S. Census, to Turing’s relay-based “Robinson” machine that cracked the Nazi enigma code, to the CBS vacuum tube computer that predicted the election of Eisenhower, to the transistor-based machines used in the first space launches, to the integrated-circuit-based personal computer which I used to dictate (and automatically transcribe) this essay.
But I noticed something else surprising. When I plotted the 49 machines on an exponential graph (where a straight line means exponential growth), I didn’t get a straight line. What I got was another exponential curve. In other words, there’s exponential growth in the rate of exponential growth. Computer speed (per unit cost) doubled every three years between 1910 and 1950, doubled every two years between 1950 and 1966, and is now doubling every year.
But where does Moore’s Law come from? What is behind this remarkably predictable phenomenon? I have seen relatively little written about the ultimate source of this trend. Is it just “a set of industry expectations and goals,” as Randy Isaac, head of basic science at IBM contends? Or is there something more profound going on?
In my view, it is one manifestation (among many) of the exponential growth of the evolutionary process that is technology. The exponential growth of computing is a marvelous quantitative example of the exponentially growing returns from an evolutionary process. We can also express the exponential growth of computing in terms of an accelerating pace: it took ninety years to achieve the first MIPS (million instructions per second) per thousand dollars, now we add one MIPS per thousand dollars every day.
Moore’s Law narrowly refers to the number of transistors on an integrated circuit of fixed size, and sometimes has been expressed even more narrowly in terms of transistor feature size. But rather than feature size (which is only one contributing factor), or even number of transistors, I think the most appropriate measure to track is computational speed per unit cost. This takes into account many levels of “cleverness” (i.e., innovation, which is to say, technological evolution). In addition to all of the innovation in integrated circuits, there are multiple layers of innovation in computer design, e.g., pipelining, parallel processing, instruction look-ahead, instruction and memory caching, and many others.
From the above chart, we see that the exponential growth of computing didn’t start with integrated circuits (around 1958), or even transistors (around 1947), but goes back to the electromechanical calculators used in the 1890 and 1900 U.S. Census. This chart spans at least five distinct paradigms of computing, of which Moore’s Law pertains to only the latest one.
It’s obvious what the sixth paradigm will be after Moore’s Law runs out of steam during the second decade of this century. Chips today are flat (although it does require up to 20 layers of material to produce one layer of circuitry). Our brain, in contrast, is organized in three dimensions. We live in a three dimensional world, why not use the third dimension? The human brain actually uses a very inefficient electrochemical digital controlled analog computational process. The bulk of the calculations are done in the interneuronal connections at a speed of only about 200 calculations per second (in each connection), which is about ten million times slower than contemporary electronic circuits. But the brain gains its prodigious powers from its extremely parallel organization in three dimensions. There are many technologies in the wings that build circuitry in three dimensions. Nanotubes, for example, which are already working in laboratories, build circuits from pentagonal arrays of carbon atoms. One cubic inch of nanotube circuitry would be a million times more powerful than the human brain. There are more than enough new computing technologies now being researched, including three-dimensional silicon chips, optical computing, crystalline computing, DNA computing, and quantum computing, to keep the law of accelerating returns as applied to computation going for a long time.
Thus the (double) exponential growth of computing is broader than Moore’s Law, which refers to only one of its paradigms. And this accelerating growth of computing is, in turn, part of the yet broader phenomenon of the accelerating pace of any evolutionary process. Observers are quick to criticize extrapolations of an exponential trend on the basis that the trend is bound to run out of “resources.” The classical example is when a species happens upon a new habitat (e.g., rabbits in Australia), the species’ numbers will grow exponentially for a time, but then hit a limit when resources such as food and space run out.
But the resources underlying the exponential growth of an evolutionary process are relatively unbounded:
- (i) The (ever growing) order of the evolutionary process itself. Each stage of evolution provides more powerful tools for the next. In biological evolution, the advent of DNA allowed more powerful and faster evolutionary “experiments.” Later, setting the “designs” of animal body plans during the Cambrian explosion allowed rapid evolutionary development of other body organs such as the brain. Or to take a more recent example, the advent of computer assisted design tools allows rapid development of the next generation of computers.
- (ii) The “chaos” of the environment in which the evolutionary process takes place and which provides the options for further diversity. In biological evolution, diversity enters the process in the form of mutations and ever changing environmental conditions. In technological evolution, human ingenuity combined with ever changing market conditions keep the process of innovation going.
The maximum potential of matter and energy to contain intelligent processes is a valid issue. But according to my models, we won’t approach those limits during this century (but this will become an issue within a couple of centuries).
We also need to distinguish between the “S” curve (an “S” stretched to the right, comprising very slow, virtually unnoticeable growth–followed by very rapid growth–followed by a flattening out as the process approaches an asymptote) that is characteristic of any specific technological paradigm and the continuing exponential growth that is characteristic of the ongoing evolutionary process of technology. Specific paradigms, such as Moore’s Law, do ultimately reach levels at which exponential growth is no longer feasible. Thus Moore’s Law is an S curve. But the growth of computation is an ongoing exponential (at least until we “saturate” the Universe with the intelligence of our human-machine civilization, but that will not be a limit in this coming century). In accordance with the law of accelerating returns, paradigm shift, also called innovation, turns the S curve of any specific paradigm into a continuing exponential. A new paradigm (e.g., three-dimensional circuits) takes over when the old paradigm approaches its natural limit. This has already happened at least four times in the history of computation. This difference also distinguishes the tool making of non-human species, in which the mastery of a tool-making (or using) skill by each animal is characterized by an abruptly ending S shaped learning curve, versus human-created technology, which has followed an exponential pattern of growth and acceleration since its inception.
DNA Sequencing, Memory, Communications, the Internet, and Miniaturization
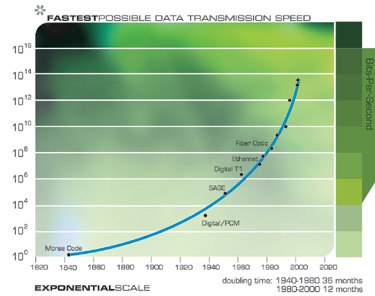
This “law of accelerating returns” applies to all of technology, indeed to any true evolutionary process, and can be measured with remarkable precision in information based technologies. There are a great many examples of the exponential growth implied by the law of accelerating returns in technologies as varied as DNA sequencing, communication speeds, electronics of all kinds, and even in the rapidly shrinking size of technology. The Singularity results not from the exponential explosion of computation alone, but rather from the interplay and myriad synergies that will result from manifold intertwined technological revolutions. Also, keep in mind that every point on the exponential growth curves underlying these panoply of technologies (see the graphs below) represents an intense human drama of innovation and competition. It is remarkable therefore that these chaotic processes result in such smooth and predictable exponential trends.
For example, when the human genome scan started fourteen years ago, critics pointed out that given the speed with which the genome could then be scanned, it would take thousands of years to finish the project. Yet the fifteen year project was nonetheless completed slightly ahead of schedule.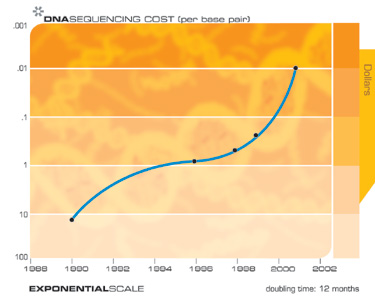
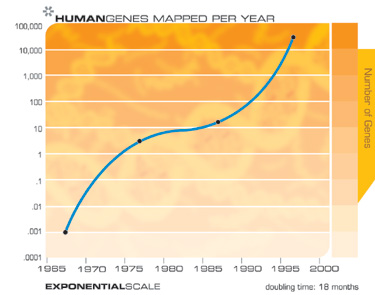

Of course, we expect to see exponential growth in electronic memories such as RAM.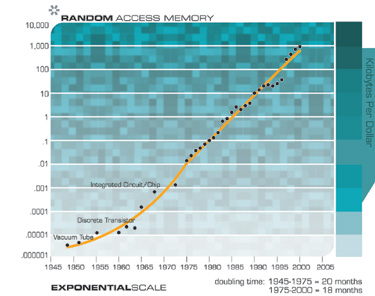
Notice How Exponential Growth Continued through Paradigm Shifts from Vacuum Tubes to Discrete Transistors to Integrated Circuits
However, growth in magnetic memory is not primarily a matter of Moore’s law, but includes advances in mechanical and electromagnetic systems.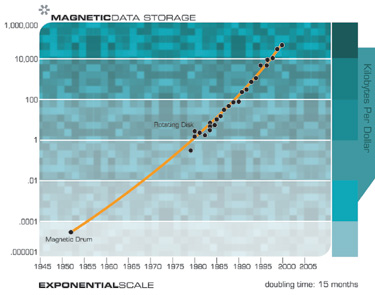
Exponential growth in communications technology has been even more explosive than in computation and is no less significant in its implications. Again, this progression involves far more than just shrinking transistors on an integrated circuit, but includes accelerating advances in fiber optics, optical switching, electromagnetic technologies, and others.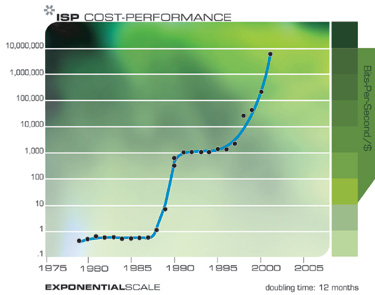
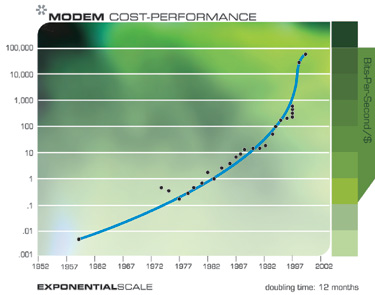
Notice Cascade of smaller “S” Curves
Note that in the above two charts we can actually see the progression of “S” curves: the acceleration fostered by a new paradigm, followed by a leveling off as the paradigm runs out of steam, followed by renewed acceleration through paradigm shift.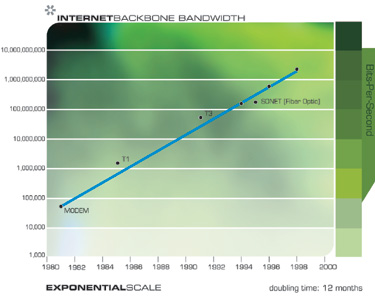
The following two charts show the overall growth of the Internet based on the number of hosts. These two charts plot the same data, but one is on an exponential axis and the other is linear. As I pointed out earlier, whereas technology progresses in the exponential domain, we experience it in the linear domain. So from the perspective of most observers, nothing was happening until the mid 1990s when seemingly out of nowhere, the world wide web and email exploded into view. But the emergence of the Internet into a worldwide phenomenon was readily predictable much earlier by examining the exponential trend data.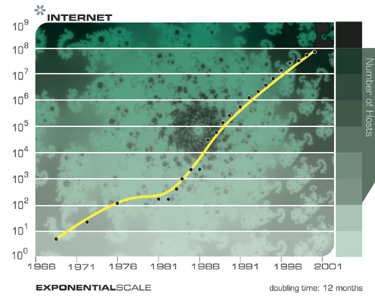
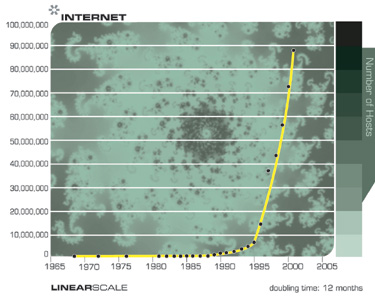
Notice how the explosion of the Internet appears to be a surprise from the Linear Chart, but was perfectly predictable from the Exponential Chart
Ultimately we will get away from the tangle of wires in our cities and in our lives through wireless communication, the power of which is doubling every 10 to 11 months.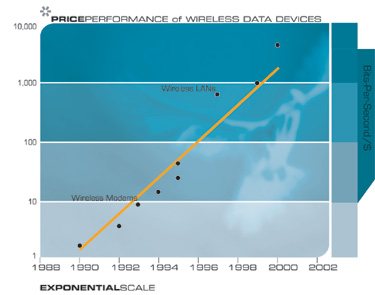
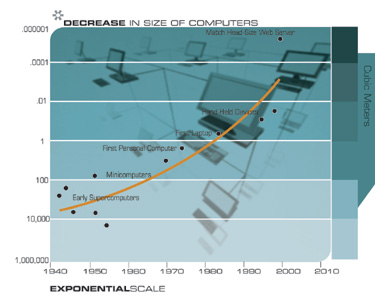
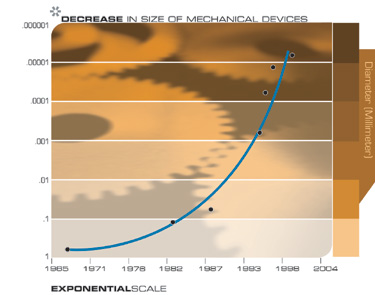
Another technology that will have profound implications for the twenty-first century is the pervasive trend toward making things smaller, i.e., miniaturization. The salient implementation sizes of a broad range of technologies, both electronic and mechanical, are shrinking, also at a double exponential rate. At present, we are shrinking technology by a factor of approximately 5.6 per linear dimension per decade.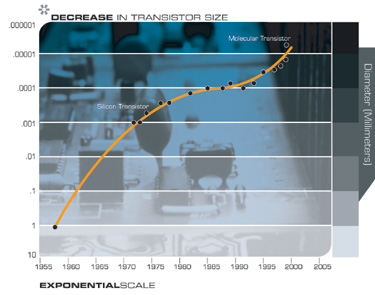
The Exponential Growth of Computation Revisited
If we view the exponential growth of computation in its proper perspective as one example of the pervasiveness of the exponential growth of information based technology, that is, as one example of many of the law of accelerating returns, then we can confidently predict its continuation.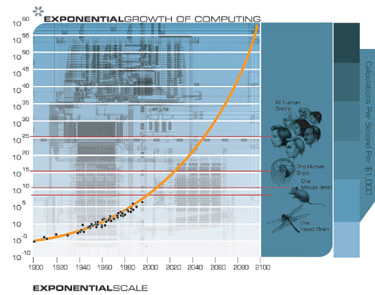
In the accompanying sidebar, I include a simplified mathematical model of the law of accelerating returns as it pertains to the (double) exponential growth of computing. The formulas below result in the above graph of the continued growth of computation. This graph matches the available data for the twentieth century through all five paradigms and provides projections for the twenty-first century. Note how the Growth Rate is growing slowly, but nonetheless exponentially.
The Law of Accelerating Returns Applied to the Growth of Computation
The following provides a brief overview of the law of accelerating returns as it applies to the double exponential growth of computation. This model considers the impact of the growing power of the technology to foster its own next generation. For example, with more powerful computers and related technology, we have the tools and the knowledge to design yet more powerful computers, and to do so more quickly.
Note that the data for the year 2000 and beyond assume neural net connection calculations as it is expected that this type of calculation will ultimately dominate, particularly in emulating human brain functions. This type of calculation is less expensive than conventional (e.g., Pentium III / IV) calculations by a factor of at least 100 (particularly if implemented using digital controlled analog electronics, which would correspond well to the brain’s digital controlled analog electrochemical processes). A factor of 100 translates into approximately 6 years (today) and less than 6 years later in the twenty-first century.
My estimate of brain capacity is 100 billion neurons times an average 1,000 connections per neuron (with the calculations taking place primarily in the connections) times 200 calculations per second. Although these estimates are conservatively high, one can find higher and lower estimates. However, even much higher (or lower) estimates by orders of magnitude only shift the prediction by a relatively small number of years.
Some prominent dates from this analysis include the following:
- We achieve one Human Brain capability (2 * 10^16 cps) for $1,000 around the year 2023.
- We achieve one Human Brain capability (2 * 10^16 cps) for one cent around the year 2037.
- We achieve one Human Race capability (2 * 10^26 cps) for $1,000 around the year 2049.
- We achieve one Human Race capability (2 * 10^26 cps) for one cent around the year 2059.
The Model considers the following variables:
- V: Velocity (i.e., power) of computing (measured in CPS/unit cost)
- W: World Knowledge as it pertains to designing and building computational devices
- t: Time
The assumptions of the model are:
- (1) V = C1 * W
In other words, computer power is a linear function of the knowledge of how to build computers. This is actually a conservative assumption. In general, innovations improve V (computer power) by a multiple, not in an additive way. Independent innovations multiply each other’s effect. For example, a circuit advance such as CMOS, a more efficient IC wiring methodology, and a processor innovation such as pipelining all increase V by independent multiples.
- (2) W = C2 * Integral (0 to t) V
In other words, W (knowledge) is cumulative, and the instantaneous increment to knowledge is proportional to V.
This gives us:
- W = C1 * C2 * Integral (0 to t) W
- W = C1 * C2 * C3 ^ (C4 * t)
- V = C1 ^ 2 * C2 * C3 ^ (C4 * t)
- (Note on notation: a^b means a raised to the b power.)
Simplifying the constants, we get:
- V = Ca * Cb ^ (Cc * t)
So this is a formula for “accelerating” (i.e., exponentially growing) returns, a “regular Moore’s Law.”
As I mentioned above, the data shows exponential growth in the rate of exponential growth. (We doubled computer power every three years early in the twentieth century, every two years in the middle of the century, and close to every one year during the 1990s.)
Let’s factor in another exponential phenomenon, which is the growing resources for computation. Not only is each (constant cost) device getting more powerful as a function of W, but the resources deployed for computation are also growing exponentially.
We now have:
- N: Expenditures for computation
- V = C1 * W (as before)
- N = C4 ^ (C5 * t) (Expenditure for computation is growing at its own exponential rate)
- W = C2 * Integral(0 to t) (N * V)
As before, world knowledge is accumulating, and the instantaneous increment is proportional to the amount of computation, which equals the resources deployed for computation (N) * the power of each (constant cost) device.
This gives us:
- W = C1 * C2 * Integral(0 to t) (C4 ^ (C5 * t) * W)
- W = C1 * C2 * (C3 ^ (C6 * t)) ^ (C7 * t)
- V = C1 ^ 2 * C2 * (C3 ^ (C6 * t)) ^ (C7 * t)
Simplifying the constants, we get:
- V = Ca * (Cb ^ (Cc * t)) ^ (Cd * t)
This is a double exponential–an exponential curve in which the rate of exponential growth is growing at a different exponential rate.
Now let’s consider real-world data. Considering the data for actual calculating devices and computers during the twentieth century:
- CPS/$1K: Calculations Per Second for $1,000
Twentieth century computing data matches:
- CPS/$1K = 10^(6.00*((20.40/6.00)^((A13-1900)/100))-11.00)
We can determine the growth rate over a period of time:
- Growth Rate =10^((LOG(CPS/$1K for Current Year) – LOG(CPS/$1K for Previous Year))/(Current Year – Previous Year))
- Human Brain = 100 Billion (10^11) neurons * 1000 (10^3) Connections/Neuron * 200 (2 * 10^2) Calculations Per Second Per Connection = 2 * 10^16 Calculations Per Second
- Human Race = 10 Billion (10^10) Human Brains = 2 * 10^26 Calculations Per Second
These formulas produce the graph above.
Already, IBM’s “Blue Gene” supercomputer, now being built and scheduled to be completed by 2005, is projected to provide 1 million billion calculations per second (i.e., one billion megaflops). This is already one twentieth of the capacity of the human brain, which I estimate at a conservatively high 20 million billion calculations per second (100 billion neurons times 1,000 connections per neuron times 200 calculations per second per connection). In line with my earlier predictions, supercomputers will achieve one human brain capacity by 2010, and personal computers will do so by around 2020. By 2030, it will take a village of human brains (around a thousand) to match $1000 of computing. By 2050, $1000 of computing will equal the processing power of all human brains on Earth. Of course, this only includes those brains still using carbon-based neurons. While human neurons are wondrous creations in a way, we wouldn’t (and don’t) design computing circuits the same way. Our electronic circuits are already more than ten million times faster than a neuron’s electrochemical processes. Most of the complexity of a human neuron is devoted to maintaining its life support functions, not its information processing capabilities. Ultimately, we will need to port our mental processes to a more suitable computational substrate. Then our minds won’t have to stay so small, being constrained as they are today to a mere hundred trillion neural connections each operating at a ponderous 200 digitally controlled analog calculations per second.
The Software of Intelligence
So far, I’ve been talking about the hardware of computing. The software is even more salient. One of the principal assumptions underlying the expectation of the Singularity is the ability of nonbiological mediums to emulate the richness, subtlety, and depth of human thinking. Achieving the computational capacity of the human brain, or even villages and nations of human brains will not automatically produce human levels of capability. By human levels I include all the diverse and subtle ways in which humans are intelligent, including musical and artistic aptitude, creativity, physically moving through the world, and understanding and responding appropriately to emotion. The requisite hardware capacity is a necessary but not sufficient condition. The organization and content of these resources–the software of intelligence–is also critical.
Before addressing this issue, it is important to note that once a computer achieves a human level of intelligence, it will necessarily soar past it. A key advantage of nonbiological intelligence is that machines can easily share their knowledge. If I learn French, or read War and Peace, I can’t readily download that learning to you. You have to acquire that scholarship the same painstaking way that I did. My knowledge, embedded in a vast pattern of neurotransmitter concentrations and interneuronal connections, cannot be quickly accessed or transmitted. But we won’t leave out quick downloading ports in our nonbiological equivalents of human neuron clusters. When one computer learns a skill or gains an insight, it can immediately share that wisdom with billions of other machines.
As a contemporary example, we spent years teaching one research computer how to recognize continuous human speech. We exposed it to thousands of hours of recorded speech, corrected its errors, and patiently improved its performance. Finally, it became quite adept at recognizing speech (I dictated most of my recent book to it). Now if you want your own personal computer to recognize speech, it doesn’t have to go through the same process; you can just download the fully trained patterns in seconds. Ultimately, billions of nonbiological entities can be the master of all human and machine acquired knowledge.
In addition, computers are potentially millions of times faster than human neural circuits. A computer can also remember billions or even trillions of facts perfectly, while we are hard pressed to remember a handful of phone numbers. The combination of human level intelligence in a machine with a computer’s inherent superiority in the speed, accuracy, and sharing ability of its memory will be formidable.
There are a number of compelling scenarios to achieve higher levels of intelligence in our computers, and ultimately human levels and beyond. We will be able to evolve and train a system combining massively parallel neural nets with other paradigms to understand language and model knowledge, including the ability to read and model the knowledge contained in written documents. Unlike many contemporary “neural net” machines, which use mathematically simplified models of human neurons, some contemporary neural nets are already using highly detailed models of human neurons, including detailed nonlinear analog activation functions and other relevant details. Although the ability of today’s computers to extract and learn knowledge from natural language documents is limited, their capabilities in this domain are improving rapidly. Computers will be able to read on their own, understanding and modeling what they have read, by the second decade of the twenty-first century. We can then have our computers read all of the world’s literature–books, magazines, scientific journals, and other available material. Ultimately, the machines will gather knowledge on their own by venturing out on the web, or even into the physical world, drawing from the full spectrum of media and information services, and sharing knowledge with each other (which machines can do far more easily than their human creators).
Reverse Engineering the Human Brain
The most compelling scenario for mastering the software of intelligence is to tap into the blueprint of the best example we can get our hands on of an intelligent process. There is no reason why we cannot reverse engineer the human brain, and essentially copy its design. Although it took its original designer several billion years to develop, it’s readily available to us, and not (yet) copyrighted. Although there’s a skull around the brain, it is not hidden from our view.
The most immediately accessible way to accomplish this is through destructive scanning: we take a frozen brain, preferably one frozen just slightly before rather than slightly after it was going to die anyway, and examine one brain layer–one very thin slice–at a time. We can readily see every neuron and every connection and every neurotransmitter concentration represented in each synapse-thin layer.
Human brain scanning has already started. A condemned killer allowed his brain and body to be scanned and you can access all 10 billion bytes of him on the Internet http://www.nlm.nih.gov/research/visible/visible_human.html.
He has a 25 billion byte female companion on the site as well in case he gets lonely. This scan is not high enough in resolution for our purposes, but then, we probably don’t want to base our templates of machine intelligence on the brain of a convicted killer, anyway.
But scanning a frozen brain is feasible today, albeit not yet at a sufficient speed or bandwidth, but again, the law of accelerating returns will provide the requisite speed of scanning, just as it did for the human genome scan. Carnegie Mellon University’s Andreas Nowatzyk plans to scan the nervous system of the brain and body of a mouse with a resolution of less than 200 nanometers, which is getting very close to the resolution needed for reverse engineering.
We also have noninvasive scanning techniques today, including high-resolution magnetic resonance imaging (MRI) scans, optical imaging, near-infrared scanning, and other technologies which are capable in certain instances of resolving individual somas, or neuron cell bodies. Brain scanning technologies are also increasing their resolution with each new generation, just what we would expect from the law of accelerating returns. Future generations will enable us to resolve the connections between neurons and to peer inside the synapses and record the neurotransmitter concentrations.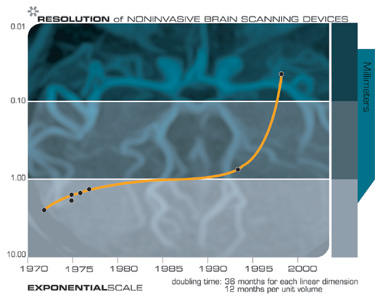
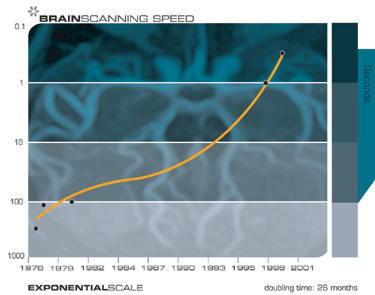
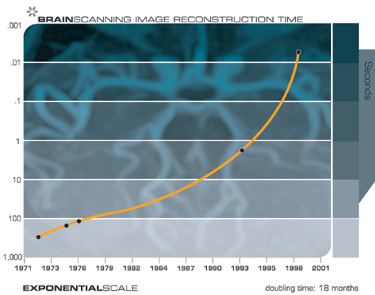
We can peer inside someone’s brain today with noninvasive scanners, which are increasing their resolution with each new generation of this technology. There are a number of technical challenges in accomplishing this, including achieving suitable resolution, bandwidth, lack of vibration, and safety. For a variety of reasons it is easier to scan the brain of someone recently deceased than of someone still living. It is easier to get someone deceased to sit still, for one thing. But noninvasively scanning a living brain will ultimately become feasible as MRI, optical, and other scanning technologies continue to improve in resolution and speed.
Scanning from Inside
Although noninvasive means of scanning the brain from outside the skull are rapidly improving, the most practical approach to capturing every salient neural detail will be to scan it from inside. By 2030, “nanobot” (i.e., nano robot) technology will be viable, and brain scanning will be a prominent application. Nanobots are robots that are the size of human blood cells, or even smaller. Billions of them could travel through every brain capillary and scan every relevant feature from up close. Using high speed wireless communication, the nanobots would communicate with each other, and with other computers that are compiling the brain scan data base (in other words, the nanobots will all be on a wireless local area network).
This scenario involves only capabilities that we can touch and feel today. We already have technology capable of producing very high resolution scans, provided that the scanner is physically proximate to the neural features. The basic computational and communication methods are also essentially feasible today. The primary features that are not yet practical are nanobot size and cost. As I discussed above, we can project the exponentially declining cost of computation, and the rapidly declining size of both electronic and mechanical technologies. We can conservatively expect, therefore, the requisite nanobot technology by around 2030. Because of its ability to place each scanner in very close physical proximity to every neural feature, nanobot-based scanning will be more practical than scanning the brain from outside.
How to Use Your Brain Scan
How will we apply the thousands of trillions of bytes of information derived from each brain scan? One approach is to use the results to design more intelligent parallel algorithms for our machines, particularly those based on one of the neural net paradigms. With this approach, we don’t have to copy every single connection. There is a great deal of repetition and redundancy within any particular brain region. Although the information contained in a human brain would require thousands of trillions of bytes of information (on the order of 100 billion neurons times an average of 1,000 connections per neuron, each with multiple neurotransmitter concentrations and connection data), the design of the brain is characterized by a human genome of only about a billion bytes.
Furthermore, most of the genome is redundant, so the initial design of the brain is characterized by approximately one hundred million bytes, about the size of Microsoft Word. Of course, the complexity of our brains greatly increases as we interact with the world (by a factor of more than ten million). Because of the highly repetitive patterns found in each specific brain region, it is not necessary to capture each detail in order to reverse engineer the significant digital-analog algorithms. With this information, we can design simulated nets that operate similarly. There are already multiple efforts under way to scan the human brain and apply the insights derived to the design of intelligent machines.
The pace of brain reverse engineering is only slightly behind the availability of the brain scanning and neuron structure information. A contemporary example is a comprehensive model of a significant portion of the human auditory processing system that Lloyd Watts (www.lloydwatts.com) has developed from both neurobiology studies of specific neuron types and brain interneuronal connection information. Watts’ model includes five parallel paths and includes the actual intermediate representations of auditory information at each stage of neural processing. Watts has implemented his model as real-time software which can locate and identify sounds with many of the same properties as human hearing. Although a work in progress, the model illustrates the feasibility of converting neurobiological models and brain connection data into working simulations. Also, as Hans Moravec and others have speculated, these efficient simulations require about 1,000 times less computation than the theoretical potential of the biological neurons being simulated.
Reverse Engineering the Human Brain: Five Parallel Auditory Pathways
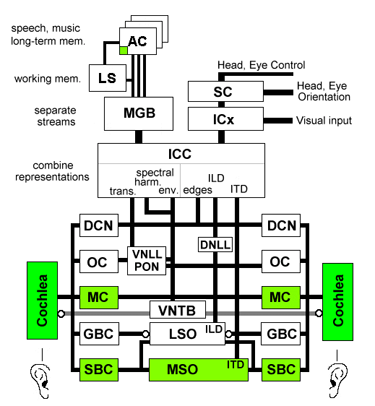
Cochlea: Sense organ of hearing. 30,000 fibers converts motion of the stapes into spectro-temporal representation of sound.
MC: Multipolar Cells. Measure spectral energy.
GBC: Globular Bushy Cells. Relays spikes from the auditory nerve to the Lateral Superior.
Olivary Complex (includes LSO and MSO). Encoding of timing and amplitude of signals for binaural comparison of level.
SBC: Spherical Bushy Cells. Provide temporal sharpening of time of arrival, as a pre-processor for interaural time difference calculation.
OC: Octopus Cells. Detection of transients.
DCN: Dorsal Cochlear Nucleus. Detection of spectral edges and calibrating for noise levels.
VNTB: Ventral Nucleus of the Trapezoid Body. Feedback signals to modulate outer hair cell function in the cochlea.
VNLL, PON: Ventral Nucleus of the Lateral Lemniscus, Peri-Olivary Nuclei. Processing transients from the Octopus Cells.
MSO: Medial Superior Olive. Computing inter-aural time difference (difference in time of arrival between the two ears, used to tell where a sound is coming from).
LSO: Lateral Superior Olive. Also involved in computing inter-aural level difference.
ICC: Central Nucleus of the Inferior Colliculus. The site of major integration of multiple representatio
Comments
Post a Comment